Векторное произведение векторов

Векторным произведением векторов $ \overline{a} $ и $ \overline{b} $ является вектор $ \overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ \overline{a} $ и $ \overline{b} $. Само произведение обозначается как $ [\overline{a},\overline{b}] $, либо $ \overline{a} \times \overline{b} $.

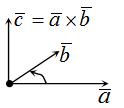
Формула векторного произведения зависит от исходных данных задачи.

Формула 1

Если известен синус угла между векторами $ \overline{a} $ и $ \overline{b} $, то найти векторное произведение векторов можно по формуле:

$$ [\overline{a},\overline{b}] = |\overline{a}| \cdot |\overline{b}| \cdot \sin (\overline{a},\overline{b}) $$

Формула 2

В случае когда векторы $ \overline{a} $ и $ \overline{b} $ заданы в координатной форме, то их произведение определяется по формуле:

$$ \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $$

где векторы $ \overline{i},\overline{j},\overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \overline{i} (a_2 b_3 - a_3 b_2) - \overline{j} (a_1 b_3 - a_3 b_1) + \overline{k} (a_1 b_2 - a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ \overline{a} \times \overline{b} = (a_2 b_3 - a_3 b_2; a_3 b_1 - a_1 b_3; a_1 b_2 - a_2 b_1) $$

Свойства

При изменении порядка множителей меняется знак на противоположный: $$ [\overline{a},\overline{b}] = -[\overline{b},\overline{a}] $$
Вынос константы за знак произведения: $$ \lambda [\overline{a},\overline{b}] = [\lambda \overline{a}, \overline{b}] = [\overline{a}, \lambda \overline{b}] $$
$$ [\overline{a}+\overline{b}, \overline{c}] = [\overline{a},\overline{c}] + [\overline{b}, \overline{c}] $$

Решение задач от 20 руб подробное решение Контрольные работы от 200 руб подробное решение

Пример 1
Найти векторное произведение векторов, заданных координатами $$ \overline{a} = (2,1,-3) $$ $$ \overline{b} = (1,2,-1) $$
Решение
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ \overline{a} $ и $ \overline{b} $: $$ \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 2&1&-3\\1&2&-1 \end{vmatrix} = \overline{i} (-1+6) - \overline{j}(-2+3) + \overline{k}(4-1) = 5\overline{i} - \overline{j} + 3\overline{k} $$ Полученный ответ можно записать в удобном виде: $$ \overline{a} \times \overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ \overline{a} \times \overline{b} = (5, -1, 3) $$

Геометрический смысл

Модуль векторного произведения векторов $ \overline{a} $ и $ \overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |\overline{a} \times \overline{b}| $$
Половина этого модуля это площадь треугольника: $$ S_\Delta = \frac{1}{2} |\overline{a} \times \overline{b} | $$
Если векторное произведение равно нулю $ \overline{a} \times \overline{b} = 0 $, то векторы коллинеарны.

Решение задач от 20 руб подробное решение Контрольные работы от 200 руб подробное решение

Пример 2
Найти площадь треугольника по заданным векторам $$ \overline{a} = (2,1,3) $$ $$ \overline{b} = (-1,2,1) $$
Решение
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ \begin{vmatrix} \overline{i}&\overline{j}&\overline{k}\\2&1&3\\-1&2&1 \end{vmatrix} = \overline{i}(1-6) - \overline{j}(2+3) + \overline{k}(4+1) = -5\overline{i} - 5\overline{j} + 5\overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ \|\overline{a} \times \overline{b}\| = \sqrt{(-5)^2 + (-5)^2 + 5^2} = \sqrt{25 + 25 + 25} = \sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_\Delta = \frac{1}{2} \|\overline{a} \times \overline{b}\| = \frac{1}{2} \sqrt{75} = 4.33 $$
Ответ
$$ S_\Delta = 4.33 $$

Нужно подробное решение своей задачи?

ЗАКАЗАТЬ РЕШЕНИЕ

Рекомендуем изучить по этой теме