Расчет трехфазной цепи переменного тока

Трехфазные цепи переменного тока представляют собой системы, состоящие из трех электрических цепей, в которых переменные токи имеют одинаковую частоту и сдвинуты по фазе относительно друг друга на 120 градусов. В основном они используются для питания трехфазных асинхронных двигателей и других мощных нагрузок.

Для расчета трехфазных цепей необходимо знать следующие параметры:

• Напряжение источника питания (линейное или фазное).
• Сопротивление нагрузки (активное, индуктивное или емкостное).
• Мощности нагрузки, которые могут быть активными, реактивными или полными.
• Коэффициент мощности нагрузки (cos φ).
• Коэффициент трансформации трансформаторов, если таковые имеются в системе.

Существует несколько методов расчета трехфазных цепей, включая метод симметричных составляющих, метод узловых напряжений, метод контурных токов и другие. Выбор метода зависит от сложности системы и требований к точности расчета. После определения всех необходимых параметров можно выполнить расчет трехфазной цепи, например, определить токи в каждой фазе, потери мощности, напряжения на нагрузке и другие параметры.

Составляется схема включения приемников

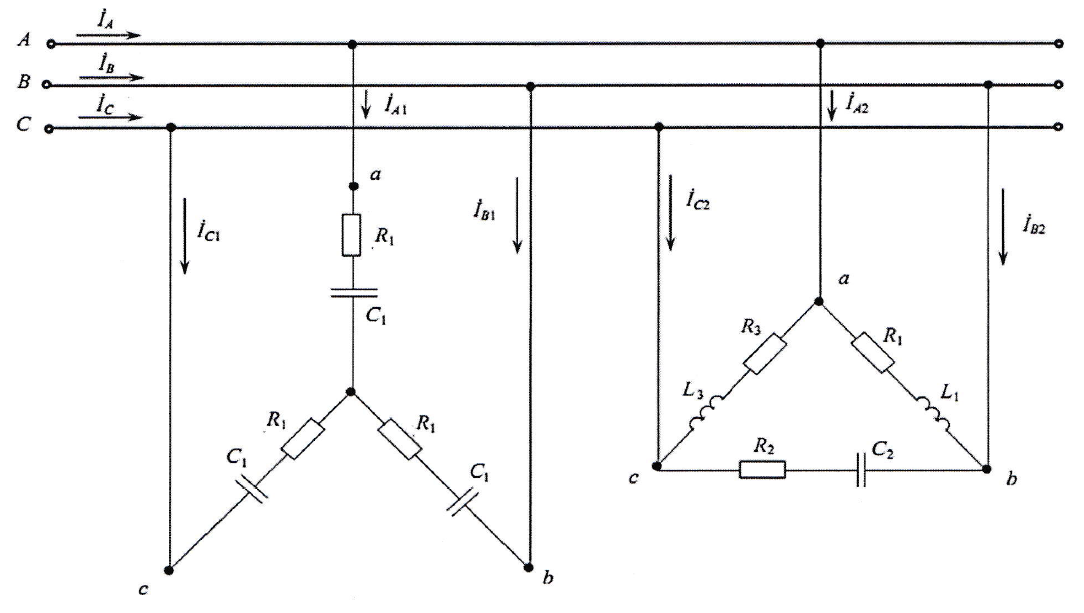
Схема соединения звезда

1. Угловая частота: $$\omega = 2\pi f = 314c^{-1}$$

2. Нагрузка всех фаз одинакова, поэтому расчет проводим для одной фазы. Определяем фазное напряжение: $$U_\phi = \frac{U_\text{л}}{\sqrt{3}} = \frac{127}{\sqrt{3}} = 73 \text{ B}$$ или в комплексной форме, принимая начальную фазу равной нулю: $$\dot{U_a} = \dot{U_A} = U_\phi e^{j0^0} = 73e^{j0^0}$$ $$\dot{U_b} = \dot{U_B} = U_\phi e^{j120^0} = 73e^{-j120^0}$$ $$\dot{U_c} = \dot{U_C} = U_\phi e^{j240^0} = 73e^{j120^0}$$

3. Нагрузка всех фаз одинакова, поэтому комплексные сопротивления всех фаз одинаковые: $$X_{C1} = \frac{1}{\omega C_1} = 39 \text{ Ом}$$ $$\underline{Z_a} = \underline{Z_b} = \underline{Z_c} = 37-j39 = 54e^{j47^0}$$

4. Для схемы соединения приемников "звезда" фазные и линейные токи равны между собой и определяются согласно закону Ома: $$\dot{I_A} = \dot{I_a} = \frac{\dot{U_a}}{\underline{Z_a}} = \frac{73e^{j0^0}}{54e^{j47^0}} = 1.4e^{-j47^0} = 1-j1$$ $$\dot{I_B} = \dot{I_b} = \frac{\dot{U_b}}{\underline{Z_b}} = \frac{73e^{-j120^0}}{54e^{j47^0}} = 1.4e^{-j167^0} = -1.4 - j0.3$$ $$\dot{U_C} = \dot{I_c} = \frac{\dot{U_c}}{\underline{Z_c}} = \frac{73e^{j120^0}}{54e^{j47^0}} = 1.4e^{j73^0} = 0.4+j1.3$$

5. Векторные диаграммы токов и напряжений:

6. Схема включения ваттметров для измерения активной мощности

7. Активная мощность, потребляемая нагрузкой: $$P = 3P_a = 3R_a I_a^2 = 218 \text{ Вт}$$

8. Реактивная мощность: $$Q=3X_a I_a^2 = -229 \text{ вар}$$

Схема соединения треугольник

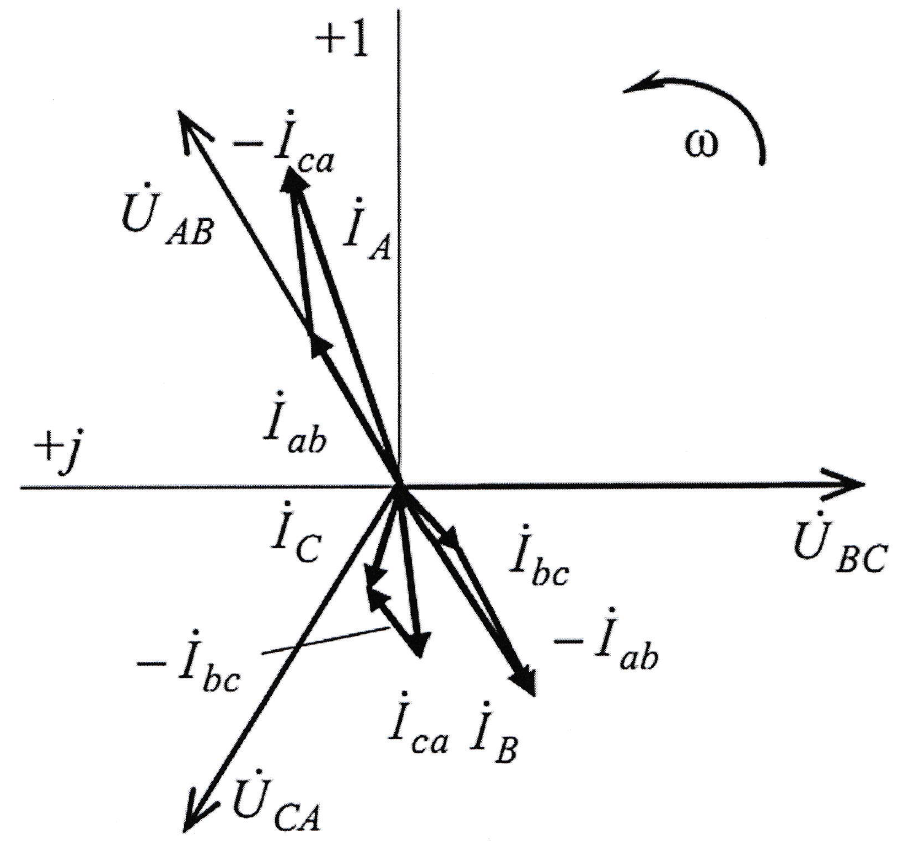
1. Напряжение сети - это линейное напряжение, кроме того, в схеме соединения "треугольник" $U_\phi = U_\text{л} = 127 \text{ B}$, то есть фазные напряжения приемников равны линейным напряжениям источников. Следовательно, система фазных напряжений приемников в комплексной форме будет иметь вид: $$\dot{U}_{AB} = \dot{U}_{ab} = U_{\text{л}} e^{j30^0} = 127e^{j30^0}$$ $$\dot{U}_{BC} = \dot{U}_{bc} = U_\text{л} e^{-j90^0} = 127 e^{-j90^0}$$ $$\dot{U_CA} = \dot{U}_{ca} = U_\text{л} e^{j150^0} = 127e^{j150^0}$$

2. Сопротивление фаз: $$X_{L_1} = \omega L_1 = 56 \text{ Ом}$$ $$X_{L_3} = \omega L_3 = 40 \text{ Ом}$$ $$X_{C_2} = \frac{1}{\omega C_2} = 52 \text{ Ом}$$ $$\underline{Z}_{ab} = 37 + j56 = 67e^{j57^0}$$ $$\underline{Z}_{bc} = 33 - j52 = 62e^{-j58^0}$$ $$\underline{Z}_{ca} = 50+j40=64e^{j51^0}$$

3. Фазные токи определяются согласну закону Ома: $$\dot{I}_{ab} = \frac{\dot{U}_{ab}}{\underline{Z}_{ab}} = \frac{127e^{j30^0}}{67e^{j57^0}} = 1.9e^{-j27^0} = 1.7 - j0.9$$ $$\dot{I}_{bc} = \frac{\dot{U}_{bc}}{\underline{Z}_{bc}} = \frac{127e^{-j90^0}}{62e^{-j58^0}} = 2.1e^{-j32^0} = 1.8-j1.1$$ $$\dot{I}_{ca} = \frac{\dot{U}_{ca}}{\underline{Z}_{ca}} = \frac{127e^{j150^0}}{64e^{j51^0}} = 2e^{j99^0} = -0.3+j2$$

4. Линейные токи определяются из фазных по первому закону Кирхгофа: $$\dot{I}_A = \dot{I}_{ab} - \dot{I}_{ca} = 1.7-j0.9-0.3-j2= $$ $$=1.4-j2.9 = 3.2e^{-j64^0}$$ $$\dot{I}_B = \dot{I}_{bc} - \dot{I}_{ab} = 1.8-j1.1 - 1.7+j0.9 = $$ $$= 0.1 - j0.2 = 0.22e^{-j64^0}$$ $$\dot{I}_C = \dot{I}_{ca} - \dot{I}_{bc} = -0.3+j2-1.8+j1.1 = $$ $$ = -2.1 + j3.1 = 3.7e^{j124^0}$$

5. Активная мощность: $$P = P_{ab} + P_{bc} + P_{ca} = R_{ab} I^2_{ab} + R_{bc} I^2_{bc} + R_{ca} I^2_{ca} = 479 \text{ Вт}$$

6. Реактивная мощность: $$Q = X_{ab} I^2_{ab} + X_{bc} I^2_{bc} + X_{ca} I^2_{ca} = 133 \text{ вар}$$

7. Векторные диаграммы токов и напряжений: