Расчет трехфазного трансформатора

1. Определим номинальные фазные напряжения при схеме соединения обмоток трансформатора по схеме "звезда-треугольник": $$U_\text{1ф.н} = \frac{U_\text{1н}}{\sqrt{3}} = \frac{6.3 \times 10^3}{\sqrt{3}} = 3637.307 \text{ B}$$ $$U_\text{2ф.н} = U_\text{2н} = 0.23 \times 10^3 \text{ B}$$

2. Определим коэффициент трансформации: $$k = \frac{U_\text{1ф.н}}{U_\text{2ф.н}} = \frac{3637.307}{230} = 15.814$$

3. Определим номинальные фазные токи первичной и вторичной обмоток: $$I_\text{1н} = \frac{S_\text{н}}{\sqrt{3}U_\text{1н}} = \frac{20 \times 10^3}{\sqrt{3} \cdot 6.3 \times 10^3} = 1.833 \text{ A}$$ $$I_\text{2н} = \frac{S_\text{н}}{\sqrt{3}U_\text{2н}} = \frac{20 \times 10^3}{\sqrt{3} \cdot 0.23 \times 10^3} = 50.204 \text{ A}$$

4. Определим параметры холостого хода схемы замещения трансформатора.

- ток холостого хода: $$I_{1xx} = \frac{i_{1xx\%}}{100\%} I_\text{1н} = \frac{9.0}{100} \cdot 1.833 = 0.165 \text{ A}$$ -сопротивления ветви намагничивания (холостого хода): $$Z_0 = \frac{U_\text{1н}}{I_\text{1xx}} = \frac{6.3 \times 10^3}{0.165} = 38191.72 \text{ Ом}$$ $$R_0 = \frac{P_x}{I_\text{1xx}^2} = \frac{180}{0.165^2} = 6615 \text{ Ом}$$ $$X_0 = \sqrt{Z_0^2 - R_0^2} = \sqrt{38191.72^2 - 6615^2} = 37614.482 \text{ Ом}$$ - коэффициент мощности холостого хода: $$\cos \varphi_0 = \frac{R_0}{Z_0} = \frac{6615}{38191.72} = 0.173$$

5. Определим параметры короткого замыкания схемы замещения трансформатора.

- напряжение короткого замыкания:$$U_\text{кз} = \frac{u_\text{к}}{100\%} U_\text{1н} = \frac{5}{100} \cdot 6300 = 315 \text{ B}$$ - сопротивления короткого замыкания: $$Z_k = \frac{U_\text{кз}}{I_\text{1н}} = \frac{315}{1.833} = 171.863 \text{ Ом}$$ $$R_k = \frac{P_k}{3I_\text{1н}^2} = \frac{600}{3\cdot 1.833^2} = 59.535 \text{ Ом}$$ $$X_k = \sqrt{Z_k^2 - R_k^2} = \sqrt{171.863^2 - 59.535^2} = 161.222 \text{ Ом}$$ - коэффициент мощности короткого замыкания: $$\cos \varphi_k = \frac{R_k}{Z_k} = \frac{59.535}{171.863} = 0.346$$

Составим Г-образную схему замещения трансформатора

7. Рассчитаем и построим внешнюю характеристику трехфазного трансформатора $U_2 = f(\beta)$ при активно-индуктивной нагрузке ($\cos \varphi_2 = 0.8$). Задаваясь значениями коэффициента нагрузки $\beta = 0.25; 0.5; 0.75; 1.0; 1.25$ определим потерю напряжения во вторичной обмотке трансформатора: $$\Delta U_2 = \beta(u_a \cos \varphi_2) + u_p \sin \varphi_2)$$, где $u_a$ и $u_p$ - соответственно активной и реактивное напряжения короткого замыкания, %: $$u_a = u_k \cos \varphi_k = 5 \cdot 0.346 = 1.732\%$$ $$u_p = \sqrt{u_k^2 - u_a^2} = \sqrt{5^2 - 1.732^2} = 4.69 \%$$

Определим напряжение холостого хода при коэффициенте нагрузки, равном 1: $$\Delta U_2 = 1.732 \cdot 0.8 + 4.69 \cdot \sqrt{1-0.8^2} = 4.2 \%$$ $$U_{2x} = \bigg (\frac{\Delta U_2 \%}{100\%} + 1 \bigg ) \cdot U_\text{2ном} = \bigg (\frac{4.2}{100} + 1 \bigg ) \cdot 230 = 239.66 \text{ B}$$

Задаваясь найденными значениями потерь напряжения, определяем напряжение на зажимах вторичной обмотки трансформатора: $$U_2 = U_{2x} \bigg (1 - \frac{\Delta U_2 \%}{100 \%} \bigg )$$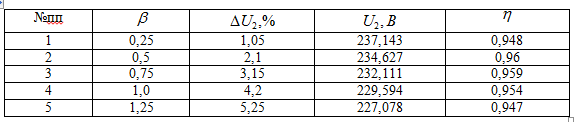

На основании табличных значений строит внешнюю характеристику $U_2 = f(\beta)$:

8. Рассчитаем и построим зависимость коэффициента полезного действия трехфазного двухобмоточного трансформатора от коэффициента нагрузки $\eta = f(\beta)$. Задаваясь значениями коэффициента нагрузки $\beta = 0.25; 0.5; 0.75; 1.0; 1.25$, определим КПД трансформатора при $\cos \varphi_2 = 0.8$: $$\eta = \frac{\beta S_\text{ном} \cos \varphi_2}{\beta S_\text{ном} \cos \varphi_2 + \beta^2 P_k + P_x}$$ На основании табличных значений зависимость КПД от нагрузки $\eta = f(\beta)$ трансформатора.