Расчет цепи однофазного переменного тока
Однофазный переменный ток является наиболее распространенным типом электричества, используемым в быту и промышленности. Он имеет ряд преимуществ перед другими видами токов, таких как простота и дешевизна генерации, передачи и потребления, а также безопасность эксплуатации. Однако при проектировании и эксплуатации электрических систем необходимо учитывать особенности расчета цепей однофазного переменного тока.
Прежде чем перейти к расчету цепей однофазного тока, необходимо разобраться с основными параметрами переменного тока. Переменный ток – это ток, который меняется по величине и направлению с течением времени. В однофазных системах переменный ток описывается следующими параметрами:
- Частота: это количество колебаний тока за одну секунду. В большинстве стран мира частота переменного тока составляет 50 или 60 Гц.
- Период: это время, за которое ток совершает одно полное колебание. Период обратно пропорционален частоте.
- Амплитуда: это максимальное значение тока в течение одного периода.
- Фаза: это положение тока в периоде. Она измеряется в градусах или радианах.
- Действующее значение: это величина, которая равна амплитуде постоянного тока, производящего такую же мощность, как и переменный ток.
Расчет цепей однофазного переменного тока имеет ряд особенностей, связанных с параметрами переменного тока и способами их представления. Для выполнения расчетов используются различные методы, включая векторные диаграммы, комплексный метод и моделирование в специализированных программах.
Расчет 1
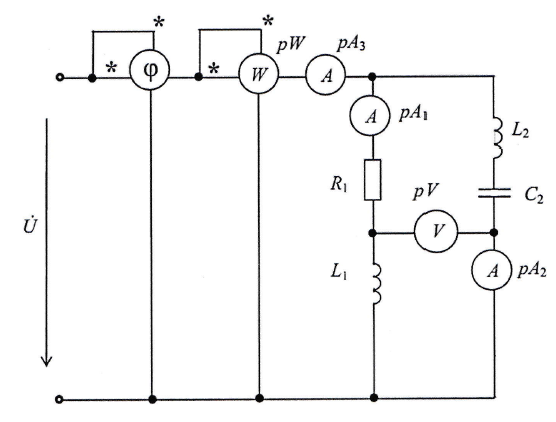

В сеть включены по приведенной схеме две ветви, требуется:
- Определить показания приборов
- Вычислить полную комплексную мощность цепи
- Построить векторные диаграммы токов и напряжений
Вычисляем угловую частоту: $$\omega = 2\pi f = 2512 c^{-1}$$
Находим реактивные сопротивления: $$X_{L_1} = \omega L_1 = 1015 \text{ Ом}$$ $$X_{L_2} = \omega L_2 = 447 \text{ Ом}$$ $$X_{C_2} = \frac{1}{\omega C_2} = 5 \text{ Ом}$$
Получаем полные комплексные сопротивления ветвей: $$\underline{Z_1} = R_1 + j(X_{L_1}) = 50+j1015 = 1016e^{j87^0}$$ $$\underline{Z_2} = j(X_{L_2} - X_{C_2}) = j442 = 442e^{j90^0}$$
Определяем комплексные токи в ветвях по закону Ома: $$\dot{I_1} = \frac{\dot{U}}{\underline{Z_1}} = \frac{200e^{j0^0}}{1016e^{j87^0}} = 0.2e^{-j87^0} = 0.01 - j0.2$$ $$\dot{I_2} = \frac{\dot{U}}{\underline{Z_2}} = \frac{200e^{j0^0}}{442e^{j90^0}} = 0.42e^{-j90^0} = -j0.42$$
Ток в неразветвленной части цепи определяется в соответствии с первым законом Кирхгофа: $$\dot{I} = \dot{I_1} + \dot{I_2} = 0.01 - j0.2 - j0.42 = 0.01 - j0.62 = 0.62e^{-j89^0}$$
Показания амперметров соответственно составят: $$pA1 \Rightarrow 0.2 A; \quad pA2 \Rightarrow 0.42 A; \quad pA3 \rightarrow 0.62 A$$
Ваттметр измеряет активную мощность, выделившуюся на активных сопротивлениях: $$P = R_1 I_1^2 = 49 \cdot 6.25 = 2 \text{ Вт}$$
Векторная диаграмма тока и напряжения:

Расчет 2


- Определите активное и реактивное сопротивление
- Вычислите величину подводимого к схеме переменного напряжения и по его значению, выполнив расчет в комплексной форме, определите показания приборов
- Постройте векторную диаграмму токов и напряжений
1. Активное сопротивление $R_4$: $$R_4 = \frac{P}{I^2} = \frac{100}{5^2} = 4 \text{ Ом}$$ Полное сопротивление $Z_4$: $$Z_4 = \frac{U}{I} = \frac{25}{5} = 5 \text{ Ом}$$ Реактивное сопротивление $X_4$: $$X_{c_4} = \sqrt{Z_4^2 - R_4^2} = \sqrt{5^2 - 4^2} = 3 \text{ Ом}$$
2. Определяем подводимое напряжение.
Рассчитаем реактивные сопротивления: $$X_{C_1} = \frac{1}{\omega \cdot C_1} = \frac{1}{314 \cdot 398 \cdot 10^{-6}} = 8 \text{ Ом}$$ $$X_{C_2} = \frac{1}{\omega \cdot C_2} = \frac{1}{314 \cdot 636.9 \cdot 10^{-6}} = 5 \text{ Ом}$$ $$X_{L_3} = \omega L_3 = 314 \cdot 35.03 \cdot 10^{-3} = 11 \text{ Ом}$$
Напряжение $\dot{U_2}$: $$\dot{U_2} = \dot{I_3} (\underline{Z_3} + \underline{Z_4}) = 5\cdot (2+j11+4-j3) = 5\cdot(6+j8) = 30+j40 = 50\angle 53.13^0 \text{ B}$$
Ток $\dot{I_2}$: $$\dot{I_2} = \frac{\dot{U_2}}{\underline{Z_2}} = \frac{30+j40}{-j5} = -8+j6 = 10\angle 143.13^0 \text{ A}$$ Ток $\dot{I_1}$: $$\dot{I_1} = \dot{I_2} + \dot{I_3} = -8+j6+5 = -3+j6=6.708 \angle 116.565^0 \text{ A}$$
Напряжение на входе: $$\dot{U} = \dot{U_1} + \dot{U_2} = 30+j60+30+j40 = 60+j100 = 116.619 \angle 59.036^0 \text{ B}$$
3. Рассчитаем токи и показания приборов для $U = 116.619 \text{ B}$: $$\dot{I_1} = \frac{\dot{U}}{\underline{Z_1} + \frac{\underline{Z_2} \cdot (\underline{Z_3} + Z_4)}{\underline{Z_2} + \underline{Z_3} + \underline{Z_4}} } = \frac{116.619}{6-j8+\frac{(-j5)\cdot (2+j11+4-j3)}{-j5+2+j11+4-j3}} = $$ $$ =3.601+j5.659 = 6.708 \angle 57.529^0 \text{ A}$$ $$\dot{I_2} = \dot{I_1} \frac{\underline{Z_3}+Z_4}{\underline{Z_2} + \underline{Z_3} + \underline{Z_4}} = (3.601+j5.659) \frac{2+j11+4-j3}{-j5+2+j11+4-j3} = $$ $$=1.029+j9.947 = 10 \angle 84.094^0 \text{ A}$$ $$\dot{I_3} = \dot{I_1} \frac{\underline{Z_2}}{\underline{Z_2}+\underline{Z_3}+\underline{Z_4}} = (3.601+j5.659)\frac{-j5}{-j5+2+j11+4-j3}= $$ $$=2.572-j4.287 = 5 \angle -59.036^0 \text{ A}$$
Показание амперметра: $$I_A = |I_3| = 5 \text{ A}$$ $$\dot{U_4} = \dot{I_3} \cdot \underline{Z_4} = (2.572 - j4.287)(4-j3) = -2.572 - j24.867 = 25 \angle -95.906^0 \text{ B}$$
Показание вольтметра: $$U_V = |\dot{U_4}| = 25 \text{ B}$$
Показание ваттметра: $$P_W = Re \{ \overset{*}{I_3} \times \dot{U_4} \} = $$ $$=Re \{(2.572+j4.287)(-2.572-j24.867)\} = Re\{100-j75\}=100$$
Действующие значения напряжений на всех элементах: $$U_{R_1} = I_1 R_1 = 40.249 \text{ B}$$ $$U_{R_3} = I_3 R_3 = 10 \text{ B}$$ $$U_{R_4} = I_3 R_4 = 20 \text{ B}$$ $$U_{C_1} = I_1 X_{C_1} = 53.666 \text{ B}$$ $$U_{C_2} = I_2 X_{C_2} = 50 \text{ B}$$ $$U_{L_3} = I_3 X_{L_3} = 55 \text{ B}$$ $$U_{C_4} = I_3 X_{C_4} = 15 \text{ B}$$
Строим векторную диаграмму:

