Интегралы для чайников
Процесс решения интегралов называется интегрированием. С помощью интегрирования можно находить некоторые физические величины: площадь, объем, массу тел и многое другое.
Интегралы бывают неопределенными и определенными. Рассмотрим вид определенного интеграла и попытаемся понять его физический смысл. Представляется он в таком виде: $$ \int ^a _b f(x) dx $$. Отличительная черта написание определенного интеграла от неопределенного в том, что есть пределы интегрирования a и b. Сейчас узнаем для чего они нужны, и что всё-таки значит определенный интеграл. В геометрическом смысле такой интеграл равен площади фигуры, ограниченной кривой f(x), линиями a и b, и осью Ох.
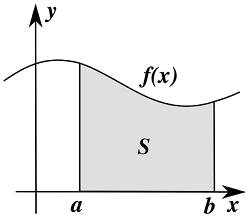
Из рис.1 видно, что определенный интеграл - это и есть та самая площадь, что закрашена серым цветом. Давайте, проверим это на простейшем примере. Найдем площадь фигуры на изображении представленном ниже с помощью интегрирования, а затем вычислим её обычным способом умножения длины на ширину.
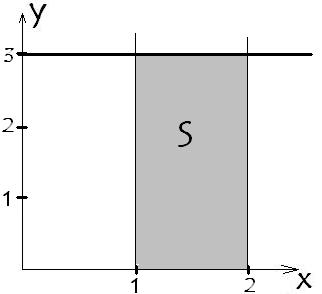
Из рис.2 видно, что $ y=f(x)=3 $, $ a=1, b=2 $. Теперь подставим их в определение интеграла, получаем, что $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2=(3 \cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text{ед}^2 $$ Сделаем проверку обычным способом. В нашем случае длина = 3, ширина фигуры = 1. $$ S = \text{длина} \cdot \text{ширина} = 3 \cdot 1 = 3 \text{ед}^2 $$ Как видим, всё отлично совпало.
Появляется вопрос: как решать интегралы неопределенные и какой у них смысл? Решение таких интегралов - это нахождение первообразных функций. Этот процесс противоположный нахождению производной. Для того, чтобы найти первообразную можно использовать нашу помощь в решении задач по математике или же необходимо самостоятельно безошибочно вызубрить свойства интегралов и таблицу интегрирования простейших элементарных функций. Нахождение выглядит так $$ \int f(x) dx = F(x) + C \text{где} F(x) $ - первообразная $ f(x), C = const $.
Для решения интеграла нужно интегрировать функцию $ f(x) $ по переменной. Если функция табличная, то записывается ответ в подходящем виде. Если же нет, то процесс сводится к получению табличной функции из функции $ f(x) $ путем хитрых математических преобразований. Для этого есть различные методы и свойства, которые рассмотрим далее.
Свойства интегралов
- Вынос константы из под знака интеграла: $$ $$ $$ \int Cg(x) dx = C\int g(x) dx $$
- Интеграл суммы/разности двух функций равен сумме/разности интегралов этих функций: $$ \int ( f(x) \pm g(x)) dx = \int f(x) dx \pm \int g(x) dx $$
- Изменение направления интегрирования: $$ \int _a ^b f(x) = -\int _b ^a f(x) dx $$
- Разбиение отрезка интегрирования: $$ \int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx $$ $$ c \in (a,b) $$
- Узнаем определенный интеграл или нет.
- Если неопределенный, то нужно найти первообразную функцию $ F(x) $ от подынтегральной $ f(x) $ с помощью математических преобразований приводящих к табличному виду функцию $ f(x) $.
- Если определенный, то нужно выполнить шаг 2, а затем подставить пределы $ а $ и $ b $ в первообразную функцию $ F(x) $. По какой формуле это сделать узнаете в статье "Формула Ньютона Лейбница".
| Пример 1 |
| $$ \int x dx $$ |
| Решение |
|
$$ \int x dx = \frac{x^2}{2} + C, C=const $$ Данный интеграл содержит под своим знаком табличную функцию, а это значит, что можно сразу записать ответ взятый из таблицы. |
| Ответ |
| $$ \int x dx = \frac{x^2}{2} + C $$ |
| Пример 2 |
| $$ \int 3xdx $$ |
| Решение |
|
$$ \int 3xdx = 3\int xdx = \frac{3x^2}{2}+C $$ Замечаем, что под знаком интеграла есть постоянная 3. По первому свойству можно ее вынести за значок интеграла. Далее, видим, что подынтегральная функция является табличной и получаем из нее первообразную для f(x)=x. |
| Ответ |
| $$ \int 3xdx = \frac{3x^2}{2}+C $$ |
| Пример 3 |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx $$ |
| Решение |
|
$$ \int (x^3+\frac{1}{2\sqrt{x}}) dx =$$ $$ = \int x^3 dx + \int \frac{1}{2\sqrt{x}}dx =$$ $$ = \frac{x^4}{4}+\sqrt{x} + C, C=const $$ Проанализировав неопределенный интеграл заметили, что подынтегральные функции являются табличными. И дана их сумма. Можно воспользоваться свойством номер 2. Значит, производим операции над функцией $ f(x) $ и $ g(x) $ согласно указанным в табличке преобразованиям. Так как интеграл неопределенный, то получаем в ответе первообразную. |
| Ответ |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx = \frac{x^4}{4}+\sqrt{x} + C $$ |
Нужно подробное решение своей задачи?
ЗАКАЗАТЬ РЕШЕНИЕ