Расчет неразветвленной цепи переменного тока
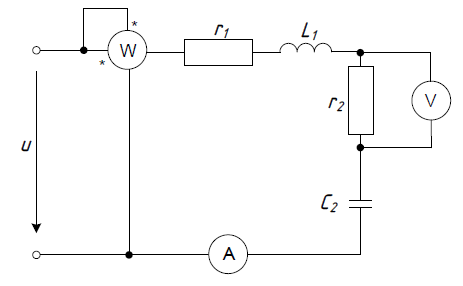
Напряжение за зажимах цепи, представленной на рисунке, изменяется по синусоидальному закону и определяется выражением $u = \sin(\omega_t + \psi_U)$. Амплитудное значение $U_m$ и начальная физа $\psi_U$ напряжения, а также значения индуктивности и емкости реактивных сопротивлений: $U_m = 180 \text{ B}, \psi_U = 30 \text{ град}, r_1 = 5 \text{ Ом}, L_1 = 0.01 \text{ Гн}, r_2 = 17 \text{ Ом}, C_2 = 250 \text{ мкФ}$.
Требуется определить:
- Определить показания приборов, указанных на схеме
- Определить закон изменения тока в цепи
- Определить закон изменения напряжения между точками, к которым подключен вольтметр
- Построить векторную диаграмму токов и напряжений
- Определить активную и реактивную мощности источника, активную и реактивную мощности приемников. Составить и оценить баланс активной и реактивной мощностей
- Определить характер (индуктивность, емкость) и параметры элемента,
который должен быть включен в цепь для того, чтобы в ней имел место
резонанс напряжений.
Определим индуктивные $x_L$ и емкостные $x_C$ сопротивления: $$x_{L1} = 2\pi f L_1 = 2\pi \cdot 50 \cdot 0.01 = 3.142 \text{ Ом}$$ $$x_{C2} = \frac{1}{2\pi f C_2} = \frac{1}{2\pi \cdot 50 \cdot 250 \cdot 10^{-6}} = 12.732 \text{ Ом}$$
Показание амперметра определяется на основе закона Ома после определения полного сопротивления цепи $$z = \sqrt{r^2 + x^2} = \sqrt{(5+17)^2 + (3.142 - 12.732)^2} = 24.0 \text{ Ом}$$ где $r$ - активное сопротивление цепи, Ом; $x$ - реактивное сопротивление цепи, Ом. $$U = \frac{U_m}{\sqrt{2}} = \frac{180}{\sqrt{2}} = 127.279 \text{ B}$$ $$I = \frac{U}{z} = \frac{127.279}{24.0} = 5.303 \text{ A}$$
Показание вольтметра определяется произведением тока на сопротивление данного участка цепи. Показание вольтметра определяется произведением тока на сопротивление данного участка цепи. Если участок содержит активное и реактивное сопротивления, то предварительно вычисляют полное сопротивление данного участка. $$U_{r_2} = I \cdot r_2 = 5.303 \cdot 17 = 90, 157 \text{ B}$$
Определяем напряжение на каждом из сопротивлений как произведение тока на соответствующее сопротивление: $$U_{x_{L1}} = I \cdot x_{L1} = 5.303 \cdot 3.142 = 16.661 \text{ B}$$ $$U_{r_1} = I \cdot r_1 = 5.303 \cdot 5 = 26.517 \text{ B}$$ $$U_{r_2} = I \cdot r_2 = 5.303 \cdot 17 = 90.157 \text{ B}$$ $$U_{x_{C2}} = I \cdot x_{c2} = 5.303 \cdot 12.732 = 67.525 \text{ B}$$
При определении закона изменения тока необходимо помнить, что он определяются законом изменения напряжения и при активно-емкостной нагрузке ток опережает напряжение на угол $\varphi$: $$\varphi = \arctg(\frac{x}{r}) = \arctg(\frac{3.142 - 12.732}{5+17}) = -23.555^0$$ $$\varphi_i = \psi_U + \varphi = 30 - 23.555 = 6.445^0$$ $$i = I_m \cdot \sin(\omega t + psi_U + \varphi) = I \cdot sqrt{2} \cdot \sin(\omega t + \psi_U + \arctg(\frac{x}{r}) = $$ $$ =5.303 \cdot \sqrt{2} \sin(\omega t + 30^0 - 23.555^0) = 7.5 \cdot \sin(\omega t + 6.445^0)$$
Закон изменения напряжения между точками, к которым подключен вольтметр определяется законом изменения тока. Закон изменения напряжения между точками, к которым подключен вольтметр, можно представить в виде уравнения: $$\varphi_U = \varphi_i - 90^0 = 6.445^0 - 90^0 = - 83.555^0$$ $$u = U_m \cdot \sin(\omega t + \varphi_U) = 180 \cdot \sin(\omega t - 83.555^0)$$
Для вычисления мощности, потребляемой цепью из сети, можно воспользоваться следующими формулами: $$S = U \cdot I = 127.279 \cdot 5.303 = 675.010 \text{ (BA)}$$ $$P = U \cdot I \cdot \cos \varphi = 127.279 \cdot 5.303 \cdot \cos(-23.555^0) = 618.768 \text{ (Bm)}$$ $$Q = U\cdot I \sin \varphi = 127.279 \cdot 5.303 \cdot \sin(-23.555^0) = -269.749 \text{ (BAp)}$$
Ваттметр измеряет активную мощность: $$P = 618.768 \text{ Bm}$$
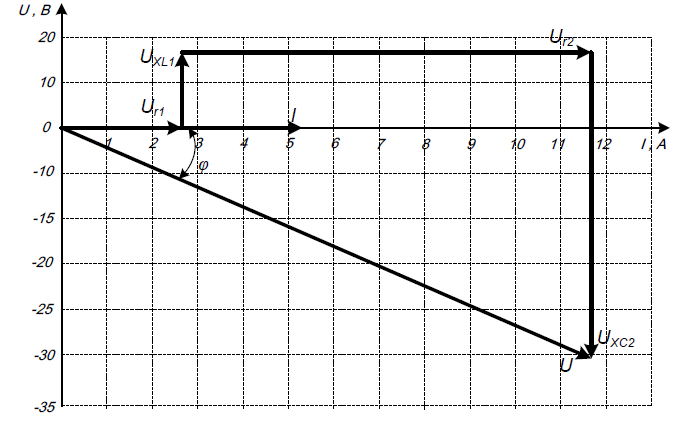
Построение векторной диаграммы для расчетной схемы проводится на основе уравнения, составленного по второму закону Кирхгофа. Выбрав масштаб тока ($m_I = 1 \text{ A/см}$) и напряжения ($m_U = 10 \text{ В/см}$), откладываем в произвольном направлении вектор тока и далее соответствующие вектора напряжений на участках цепи, учитывая, что на активном сопротивлении вектор тока и напряжения совпадают по фазе, на емкостном - вектор напряжения отстает от вектора тока на $90^0$. Результирующий вектор - это напряжение на - зажимах цепи, а угол между вектором тока и напряжения равен углу $\varphi$.
При резонансе напряжений индуктивное сопротивление $x_{L1}$ равно емкостному $x_{C2}$ и полное сопротивление $z$ становится равным активному сопротивлению $R = r_1+r_2 = 6+2 = 8 \text{ (Ом)}$. В этом случае напряжения на индуктивности $U_L$ и емкости $U_C$ равны и находятся в противофазе, поэтому при сложении они компенсируют друг друга.
Определим элемент и его величину для создания резонанса
напряжений в данной цепи. Примем, что необходимо в заданную цепь
включить индуктивность, так как сопротивление индуктивности меньше, чем
сопротивление емкости (рассчитано ранее). Рассчитаем величину
индуктивности, которая необходима для создания резонанса в заданной цепи: $$2\pi f L = \frac{1}{2\pi f C_2}$$ $$L = \frac{1}{4\pi^2 f^2 C_2} = \frac{1}{4\pi^2 \cdot 50^2 \cdot 250 \cdot 10^{-6}} = 0.041 \text{ Гн}$$
Соответственно необходимо в цепь, последовательно данным элементам включить индуктивность (катушку) величиной: $$L_{\text{доб}} = 0.041 - 0.01 = 0.031 \text{ Гн}$$
Векторная диаграмма: