Асимптоты функции
Асимптота – это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают.
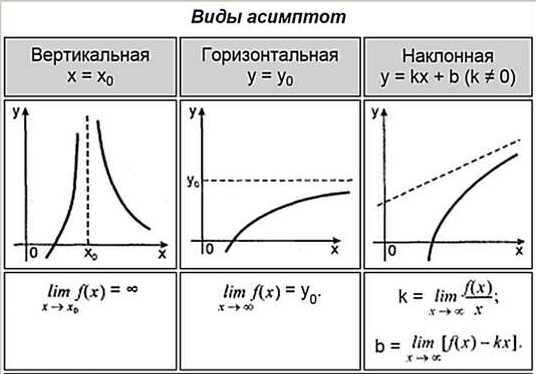
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три... и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Для нахождения вертикальных асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Для того, чтобы найти горизонтальные асимптоты, необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ - это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ \infty $, тогда наклонной асимптоты нет. А если $ k = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
Найти асимптоты графика функции $$ f(x) = \frac{5x}{3x+2} $$
Для начала решения найдем вертикальные асимптоты, но прежде найдем область определения функции $ f(x) $. По определению знаменатель не должен быть равен нулю. Поэтому имеем, $ 3x+2 \neq 0; 3x \neq -2; x \neq -\frac{2}{3} $. Получили точку разрыва $ x = -\frac{2}{3} $. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -\frac{2}{3} $.
$$ \lim\limits_{{x \rightarrow -\frac{2}{3}}} \frac{5x}{3x+2} = (-\frac{10}{0}) = -\infty $$.
Теперь найдем горизонтальные асимптоты, но прежде рассчитаем коэффициенты $ k $ и $ b $.
$$ k = \lim\limits_{x \rightarrow \infty} \frac{f(x)}{x} =\lim\limits_{x \rightarrow \infty} \frac{5}{3x+2}=\frac{5}{\infty}=0 $$
Так как $ k = 0 $, то мы уже понимаем то, что наклонных асимптот нет, а есть горизонтальные. Найдем теперь коэффициент $ b $.
$$ b = \lim\limits_{x \rightarrow \infty} [f(x)-kx] = \lim\limits_{x \rightarrow \infty} \frac{5x}{3x+2} = \frac{\infty}{\infty} =\frac{5}{3} $$
Подставляем найденные коэффициенты в формулу $ y = kx + b $, получаем, что $ y = \frac{5}{3} $ - горизонтальная асимптота.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
$$ y = \frac{5}{3} $$
Найти асимптоты функции $ f(x) = \frac{1}{1-x} $
Найдем область определения данного примера, чтобы определить вертикальные асимптоты. $ 1-x \neq 0; x \neq 1; $. Точка разрыва $ x = 1 $, а это значит что это и есть вертикальная асимптота. Найдем для доказательства предположения предел в этой точке. $$ \lim\limits_{x \rightarrow 1} \frac{1}{1-x} = \frac{1}{0} = \infty $$
Приступим к поиску наклонных асимптот.
$$ k = \lim\limits_{x \rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x \rightarrow \infty}\frac{1}{x(1-x)} = \frac{1}{\infty}=0 $$
$$ b =\lim\limits_{x \rightarrow \infty}[f(x)-kx]=\lim\limits_{x \rightarrow \infty}\frac{1}{1-x} = \frac{1}{\infty}=0 $$
Итого, $ y=0 $ - горизонтальная асимптота.
$$ y=0 $$
Найти асимптоты $f(x) = \frac{x^3}{3x^2+5} $
Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты.
$$ k = \lim\limits_{x \rightarrow \infty} \frac{f(x)}{x} =\lim\limits_{x \rightarrow \infty}\frac{x^2}{3x^2+5} =\lim\limits_{x \rightarrow \infty} \frac{2x}{6x} = \frac{1}{3} $$
Так как $ k $ конечное число, не равное $ 0 $ или бесконечности, то существует наклонная асимптота. Вычислим недостающее число $ b $.
$$ b =\lim\limits_{x \rightarrow \infty} [f(x)-kx] =\lim\limits_{x \rightarrow \infty} [\frac{x^3}{3x^2+5}-\frac{x}{3}] =\lim\limits_{x \rightarrow \infty} -\frac{5x}{3(3x^2+5)}= $$ $$ = -\frac{5}{3}\lim\limits_{x \rightarrow \infty} \frac{x}{3x^2+5} =-\frac{5}{3}\lim\limits_{x \rightarrow \infty} \frac{1}{6x} =-\frac{5}{3}\frac{1}{\infty} = 0 $$
$ y =\frac{1}{3}x $ - наклонная асимптота к функции с углом наклона одна третья.
$$ y =\frac{1}{3}x $$
Найти асимптоты графика функции $f(x) = xe^{-x} $
Нет точек разрыва, а это значит, нет вертикальных асимптот.
$$ k=\lim\limits_{x \rightarrow \infty} \frac{1}{e^x} = \frac{1}{\infty} = 0 $$
$$ b=\lim\limits_{x \rightarrow \infty} \frac{x}{e^x} =\lim\limits_{x \rightarrow \infty} \frac{1}{e^x} = \frac{1}{\infty} = 0 $$
$ y = 0 $ - горизонтальная асимптота
$$ y = 0 $$
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
