Как найти векторное произведение векторов

Векторное произведение (или векторное умножение) двух векторов a и b — это вектор c, перпендикулярный плоскости, образованной исходными векторами, с длиной, равной площади параллелограмма, построенного на этих векторах.

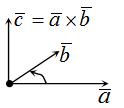
Обозначается: $$c = a \times b$$

Свойства векторного произведения

Результат — вектор (а не число, как в скалярном произведении)
Длина $|c| = |a|\cdot |b| \cdot \sin \theta$, где $\theta$ — угол между векторами
Если векторы коллинеарны ($\theta = 0$ или $180^0$), произведение равно нулю
При изменении порядка множителей меняется знак на противоположный $ (\overline{a},\overline{b}) = -(\overline{b},\overline{a}) $
Вынос константы за знак произведения $ \lambda (\overline{a},\overline{b}) = (\lambda \overline{a}, \overline{b}) = (\overline{a}, \lambda \overline{b}) $

Когда нужно векторное произведение

Применяется в:

физике (момент силы, сила Лоренца);
компьютерной графике (вычисление нормалей);
механике (определение вращательных движений);
навигации (расчёт направлений).

Пошаговый алгоритм вычисления

Запишите координаты векторов
Убедитесь, что оба вектора заданы в одной системе координат. $$a = (a_x, a_y, a_z), \space b = (b_x, b_y, b_z)$$
Составьте определитель 3×3
Первая строка: базисные векторы i,j,k.
Вторая строка: координаты a.
Третья строка: координаты b.
$$ \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} $$
Вычислите определитель
Раскройте по первой строке: $$i(a_y b_z - a_z b_y) - j(a_x b_z - a_z b_x) + k(a_x b_y - a_y b_x)$$
Выпишите результат
Коэффициенты при i,j,k дают координаты вектора c.

Примеры решений

Пример 1

Найти векторное произведение векторов $ \overline{a} = (2,1,-3)$ и $\overline{b} = (1,-2,4)$

Решение

Составляем определитель: $$ \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 2&1&-3\\1&-2&4 \end{vmatrix}$$
Вычисляем определитель: $$i(1\cdot 4−(−3) \cdot (−2))−j(2 \cdot 4−(−3) \cdot 1)+k(2 \cdot (−2)−1\cdot 1)=$$ $$=i(4−6)−j(8+3)+k(−4−1)=$$ $$=−2i−11j−5k$$
Выписываем ответ: $$a \times b = (-2; -11; -5)$$

Ответ

$$a \times b = (-2; -11; -5)$$

Решение задач от 25 руб подробное написание Контрольные работы от 200 руб подробное написание

Частые ошибки и как их избежать

Неправильный порядок векторов
$a \times b \neq b \times a$ (результат противоположен)
Совет: всегда проверяйте порядок векторов в условии задачи
Ошибки в знаках при определителе
Помните про чередование знаков: +−+
Совет: перепроверяйте знаки перед j
Путаница с координатами
Не перепутайте $x$, $y$, $z$ при записи матрицы
Совет: выписывайте координаты отдельно перед расчетом

Проверка результата

Скалярное произведение с исходными векторами
Должно быть равно нулю: $c \cdot a = 0$ и $c \cdot b = 0$
Направление
Используйте правило правой руки: большой палец по a, указательный по b, средний покажет c.