Как решать комплексные числа
Что такое комплексные числа
Комплексные числа — это числа вида $a+bi$, где $a$ и $b$ — действительные числа, а $i$ — мнимая единица, для которой выполняется равенство $i^2 = -1$.
Изображение на плоскости
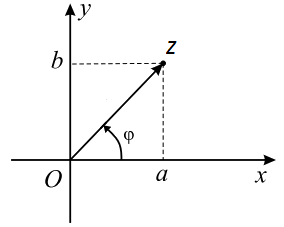 Числа $a$ и $b$ располагаются на соответствующих осях $Ox$ и $Oy$.
Числа $a$ и $b$ располагаются на соответствующих осях $Ox$ и $Oy$.
Комплексное число $ z = a+ib $ представляется в виде вектора $ \overline{z} $.
Модуль и аргумент
Модуль комплексного числа обозначается $ |z| $ и равняется длине вектора $ \overline{z} $. Рассчитывается по формуле $ |z| = \sqrt{a^2+b^2} $
Аргумент комплексного числа обозначается $ \varphi $ и рассчитывается по различным формулам в зависимости от полуплоскости, в которой лежит само число.
- $ a>0 $, то $ \varphi = arctg\frac{b}{a} $
- $ a<0, b>0 $, то $ \varphi = \pi + arctg\frac{b}{a} $
- $ a<0, b<0 $, то $ \varphi = -\pi + arctg\frac{b}{a} $
Формы записи
Существует три формы записи комплексных чисел. Можно выполнять преобразования из одной формы в другую.
- Алгебраическая $ z = a+ib $
- Показательная $ z = |z|e^{i\varphi} $
- Тригонометрическая $ z = |z|\cdot(\cos(\varphi)+i\sin(\varphi)) $
Операции с комплексными числами
Сумма и разность
$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$
$$ z_1 - z_2 = (a_1+ib_1) - (a_2+ib_2) = (a_1 - a_2)+i(b_1 - b_2) $$
Умножение
$$ z_1 \cdot z_2 = (a_1+ib_1) \cdot (a_2+ib_2) = (a_1 a_2 - b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$
Деление
$$ \frac{z_1}{z_2} = \frac{a_1+ib_1}{a_2+ib_2} = \frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i \frac{a_2 b_1 - a_1 b_2}{a_2 ^2 + b_2 ^2} $$
Возведение в степень
Формула Муавра:
$$ z^n = |z|^n(\cos n\varphi+i\sin n\varphi) $$
Извлечение корней
Формула Муавра:
$$ z^\frac{1}{n} = |z|^\frac{1}{n}\bigg(\cos \frac{\varphi + 2\pi k}{n}+i\sin \frac{\varphi + 2\pi k}{n}\bigg), k=0,1,...,n-1 $$
Примеры с решением
Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$
Для начала приступим к нахождению модуля комплексного числа:
$$ |z| = \sqrt{4^2 + (-4)^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2} $$
Осталось найти аргумент:
$$ \varphi = arctg \frac{b}{a} = arctg \frac{-4}{4} = arctg (-1) = -\frac{\pi}{4} $$
Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера:
$$ z = 4\sqrt{2}\bigg(\sin(-\frac{\pi}{4}) + i\sin(-\frac{\pi}{4}) \bigg) $$
Тут же можно записать показательную форму:
$$ z = 4\sqrt{2} e^{-\frac{\pi}{4}i} $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
$$ z = 4\sqrt{2}\bigg(\sin(-\frac{\pi}{4}) + i\sin(-\frac{\pi}{4}) \bigg) $$
$$ z = 4\sqrt{2} e^{-\frac{\pi}{4}i} $$
Вычислить сумму и разность заданных комплексных чисел:
$$ z_1 = 3+i, z_2 = 5-2i $$
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
$$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 - i $$
Аналогично выполним вычитание чисел:
$$ z_1 - z_2 = (3+i) - (5-2i) = (3-5)+(i+2i) = -2 + 3i $$
$$ z_1 + z_2 = 8 - i; z_1 - z_2 = -2 + 3i $$
Выполнить умножение и деление комплексных чисел:
$$ z_1 = 3+i, z_2 = 5-2i $$
$$ z_1 \cdot z_2 = (3+i) \cdot (5-2i) = $$
Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $:
$$ = 15 - 6i + 5i -2i^2 = 15 - i - 2\cdot(-1) = $$
$$ = 15 - i + 2 = 17 - i $$
Так, теперь разделим первое число на второе:
$$ \frac{z_1}{z_2} = \frac{3+i}{5-2i} = $$
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
$$ = \frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = \frac{15 + 6i + 5i + 2i^2}{25 + 10i - 10i -4i^2} = $$
$$ = \frac{15 + 11i -2}{25 + 4} = \frac{13 + 11i}{29} $$
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
$$ \frac{z_1}{z_2} = \frac{13}{29} + \frac{11}{29}i $$
$$ z_1 \cdot z_2 = 17 - i; \frac{z_1}{z_2} = \frac{13}{29} + \frac{11}{29}i $$
Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $
1) $ n = 2 $
Для возведения в квадрат достаточно умножить число само на себя:
$$ z^2 = (3+3i)^2 = (3+3i)\cdot (3+3i) = $$
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
$$ =9 + 9i + 3i\cdot 3 + 9i^2 = 9 + 18i - 9 = 18i $$
Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$
2) $ n = 7 $
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
$$ |z| = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} $$
Найдем чем равен аргумент:
$$ \varphi = arctg \frac{3}{3} = arctg(1) = \frac{\pi}{4} $$
Записываем в тригонометрическом виде:
$$ z = 3\sqrt{2}(\cos \frac{\pi}{4} + i\sin \frac{\pi}{4}) $$
Возводим в степень $ n = 7 $:
$$ z^7 = (3\sqrt{2})^7 (\cos \frac{7\pi}{4} + i\sin \frac{7\pi}{4}) = $$
Преобразуем в алгебраическую форму для наглядности:
$$ =(3\sqrt{2})^7 (\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}) = $$
$$ = 3^7 \sqrt{2}^7 (\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}) = $$
$$ = 3^7 \sqrt{2}^6 (1-i) = 3^7 \cdot 8(1-i) = $$
$$ = 2187 \cdot 8 (1-i) = 17496(1-i) $$
$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$
Извлечь корень $ \sqrt[3]{-1} $ над множеством $ \mathbb{C} $
Представим число в тригонометрической форме. Найдем модуль и аргумент:
$$ |z| = \sqrt{(-1)^2 + 0^2} = \sqrt{1+0} = \sqrt{1}=1 $$
$$ \varphi = arctg \frac{0}{-1} +\pi = arctg 0 + \pi = \pi $$
Получаем: $$ z = (\cos \pi + i\sin \pi) $$
Используем знакомую формулу Муавра для вычисления корней любой степени:
$$ z^\frac{1}{n} = r^\frac{1}{n}\bigg(\cos \frac{\varphi + 2\pi k}{n}+i\sin \frac{\varphi + 2\pi k}{n}\bigg), k=0,1,...,n-1 $$
Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $:
$$ z_0 = \sqrt[3]{1} (\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}) = \frac{1}{2}+i\frac{\sqrt{3}}{2} $$
$$ z_1 = \sqrt[3]{1} (\cos \frac{3\pi}{3}+i\sin \frac{3\pi}{3}) = -1 $$
$$ z_2 = \sqrt[3]{1} (\cos \frac{5\pi}{3}+i\sin \frac{5\pi}{3}) = \frac{1}{2} - i\frac{\sqrt{3}}{2} $$
$$ z_0 = \frac{1}{2}+i\frac{\sqrt{3}}{2} $$
$$ z_1 = -1 $$
$$ z_2 = \frac{1}{2} - i\frac{\sqrt{3}}{2} $$
Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ \mathbb{C} $
Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 - 4ac = 2^2 - 4\cdot 1 \cdot 2 = 4-8 = -4 $$
Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение:
$$ x_{1,2} = \frac{-b\pm \sqrt{D}}{2a} = \frac{-2\pm \sqrt{-4}}{2} = $$
Заметим, что $ \sqrt{-4} = 2\sqrt{-1} = 2i $ и продолжим вычисление:
$$ = \frac{-2 \pm 2i}{2} = -1 \pm i $$
Получили комплексно-сопряженные корни:
$$ x_1 = -1 - i; x_2 = -1 + i $$
Как видите любой многочлен можно решить благодаря комплексным числам.
$$ x_1 = -1 - i; x_2 = -1 + i $$
